티스토리 뷰
플로이드와샬 알고리즘
#include<bits/stdc++.h>
using namespace std;
int main() {
ios_base::sync_with_stdio(false);
//freopen("input.txt", "rt", stdin);
int n, m, a, b, c;
cin >> n >> m;
vector< vector <int> > dis(n+1, vector<int>(n+1, 5000));
for(int i=1; i<=n; i++) dis[i][i]=0;
for(int i=1; i<=m; i++){
cin >> a >> b >> c;
dis[a][b]=c;
}
for(int k=1; k<=n; k++){
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
dis[i][j]=min(dis[i][j], dis[i][k]+dis[k][j]);
}
}
}
for(int i=1; i<=n; i++){
for(int j=1; j<=n; j++){
if(dis[i][j]==5000) cout << "M ";
else cout << dis[i][j] << " ";
}
cout << endl;
}
return 0;
}플로이드 와샬 알고리즘을 사용해서 푸는 문제이다.
플로이드 와샬 알고리즘의 핵심은 거쳐가는 정점을 기준으로 최단거리를 구하는 것이다.
입력이 아래와 같은경우
5 8
1 2 6
1 3 3
3 2 2
2 4 1
2 5 13
3 4 5
4 2 3
4 5 7
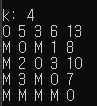
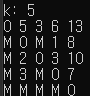
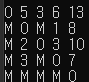
k=1일 때 i=1, j=5이라면 dis[1][5]값과 dis[1][1]+dis[1][5] 값 중 비교해서 작은 값을 dis[1][5]에 넣어준다.
기존 dis[1][5]값이 M이고 dis[1][1]+dis[1][5]=0+M이므로 여전히 dis[1][5]값은 M이다.

k=2일 때 i=1, j=5이라면 dis[1][5]값과 dis[1][2]+dis[2][5] 값 중 비교해서 작은 값을 dis[1][5]에 넣어준다.
기존 dis[1][5]값이 M이고 dis[1][2]+dis[2][5]=6+13이므로 여전히 dis[1][5]값은 19로 갱신된다.

이러한 방법으로 계속적으로 갱신하면 각 도시를 연결하는 도로들의 최소비용을 알 수 있다.

'lecture > algorithm - c++' 카테고리의 다른 글
| [c++] 위상정렬(그래프정렬) (0) | 2021.03.06 |
|---|---|
| [c++] 최대점수 구하기(냅색 알고리즘) (0) | 2021.02.20 |
| [c++] 동전교환 (0) | 2021.02.18 |
| [database] 데이터베이스 모델링 - 2 (0) | 2021.02.16 |
| [database] 데이터모델링 (0) | 2021.02.16 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 인접리스트
- javascript
- 퀵정렬
- C++
- BFS
- dfs
- 이진탐색
- 동적프로그래밍
- react
- Java
- 재귀함수
- client side rendering
- 병행프로세스
- server side rendering
- 알고리즘
- 자료구조
- 세마포어
- Stack
- 스텍
- C
- 소프트웨어
- 클래스
- 구조체
- 최단경로
- 운영체제
- 입출력장치
- 교착상태
- stackframe
- 배열
- 인접행렬
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
글 보관함
