티스토리 뷰
- 두 문자열 X와 Y사이의 편집 거리
- 두 문자열 사이의 근접성 또는 유사성을 판단하는 척도
- X = x1x2x3 ... xn, Y = y1y2 ... ym
- 문자열 X를 Y로 변환하는 데 필요한 전체 편집 연산에 대한 최소 비용
- 특정 위치에 새 문자를 삽입하는 연산 -> 삽입 비용
- 특정 위치의 문자를 삭제하는 연산 -> 삭제 비용
- 특정 위치의 문자를 다른 문자로 변경하는 연산 -> 변경 비용
- 최적성의 원리
- X와 Y사이의 편집거리는 이들의 부분 문자열 사이의 편집 거리를 포함
- Xi = x1x2 ... xi와 Yi = y1y2 ... yj 사이의 편집 거리


- 성능
- 삭제할 때 성능: O(n)
- 삽입할 때 성능: O(n)
- 변경할 때 성능: O(nm)
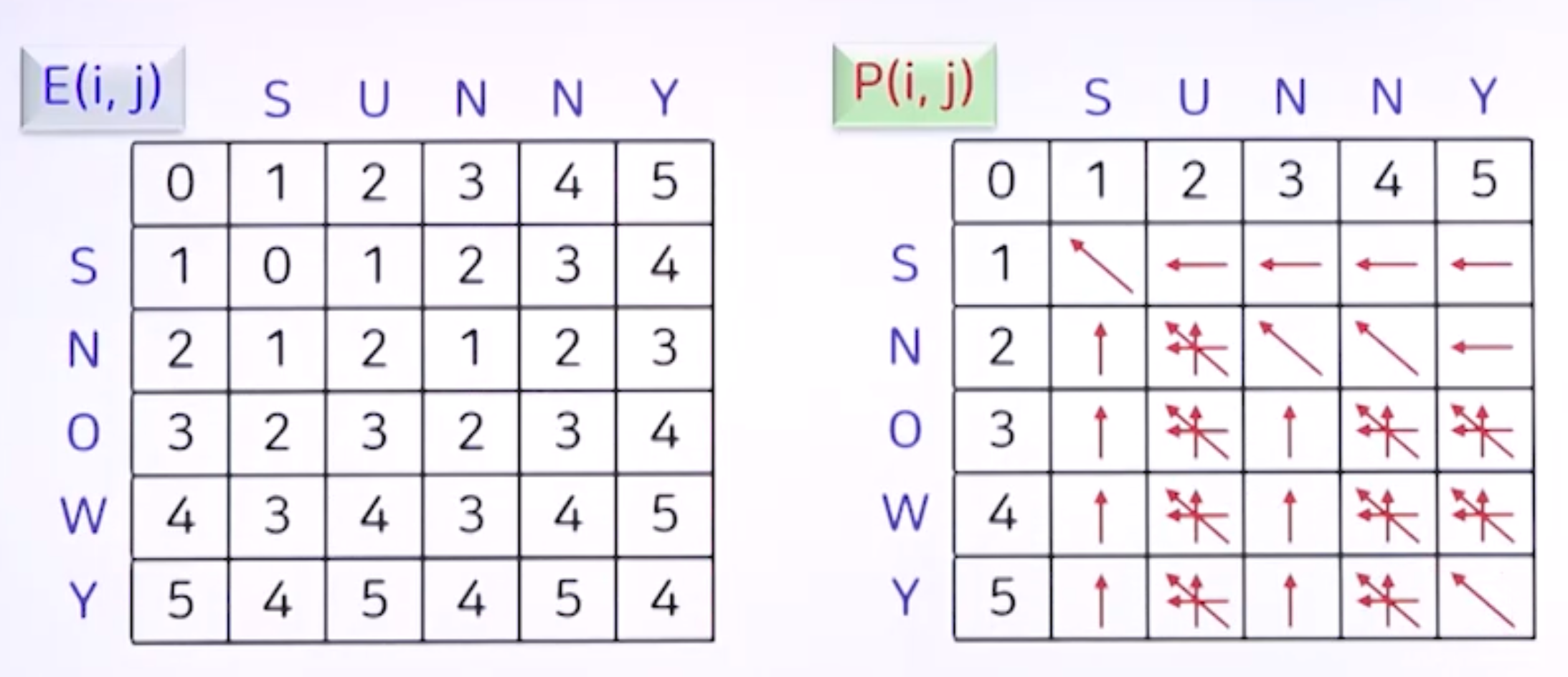
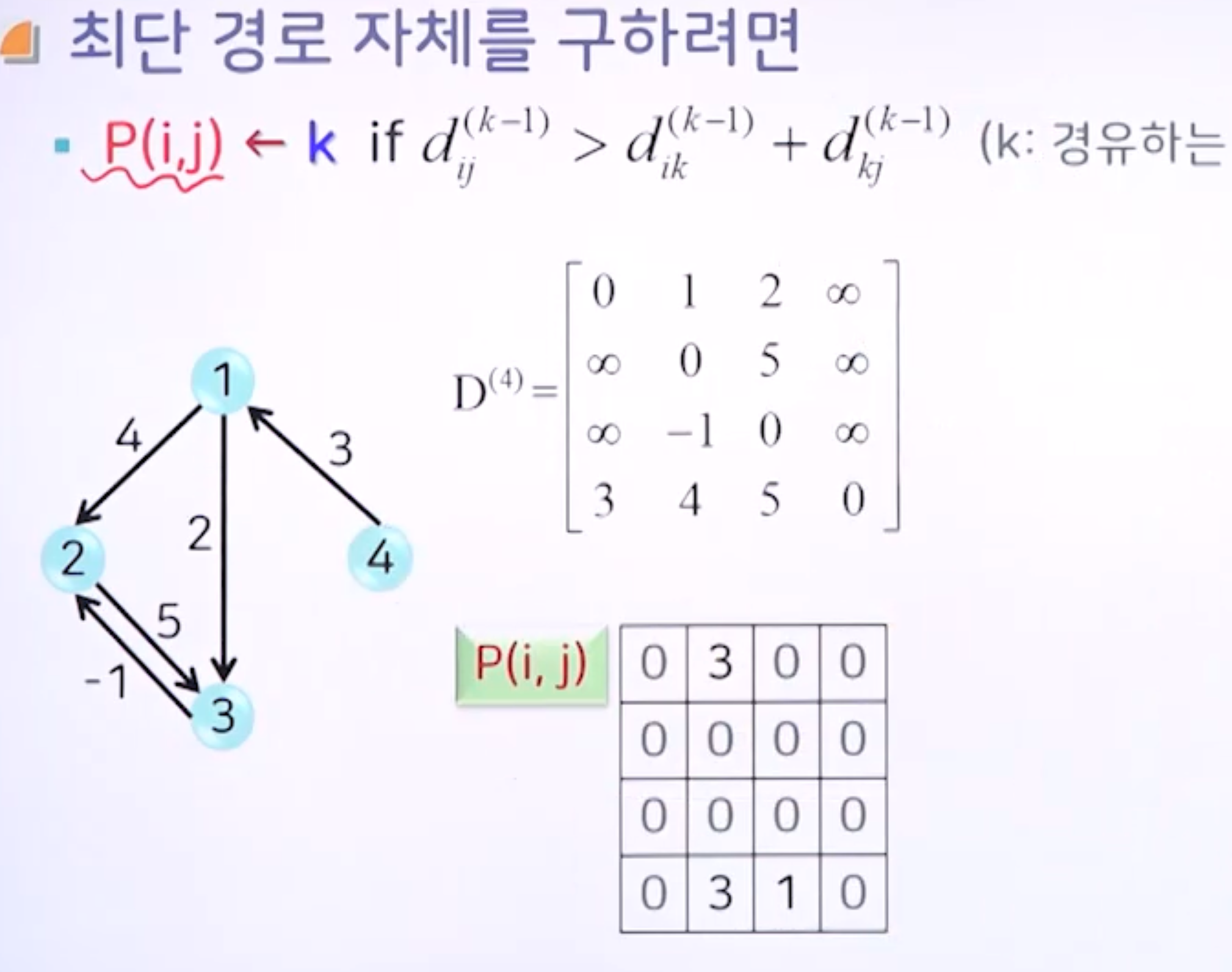
- P(i, j)
- E(i, j)로 선택되는 최소값이 어떤 연산으로 결정되는 지를 표시
- 적용된 편집 연산을 구할 수 있음
- 두 정점 간의 최단 경로
- 가중 방향 그래프에서 두 정점을 연결하는 경로 중에서 간선의 가중치의 합이 가장 작은 경로
- 유형
- 단일 출발점 최단 경로 -> 하나의 특정 정점에서 다른 모든 정점으로의 최단 경로
- 데이트스트라(Dijkstra) 알고리즘
- 모든 정점 간의 최단 경로 -> 모든 조합의 두 정점 간의 최단 경로
- 플로이드 알고리즘
- 동적 프로그래밍 방법 적용
- 가정 -> 가중치의 합이 음수인 사이클이 존재하지 않음
- 경유할 수 있는 정점의 범위가 1인 경로부터 시작해서 |V| 까지인 경로까지 하나씩 범위를 늘려가면서 모든 정점 간의 최단 경로를 한꺼번에 구하는 알고리즘
- 인접 행렬 D(k) = (dij^(k)) k = 0, 1, ..., |V|
- dij^(k)
- 정점 i에서 정점 j까지의 경로 중에서 정점 1부터 k까지의 정점만을 경유할 수 있는 최단 경로
- dij^(k)
- 플로이드 알고리즘
- 단일 출발점 최단 경로 -> 하나의 특정 정점에서 다른 모든 정점으로의 최단 경로
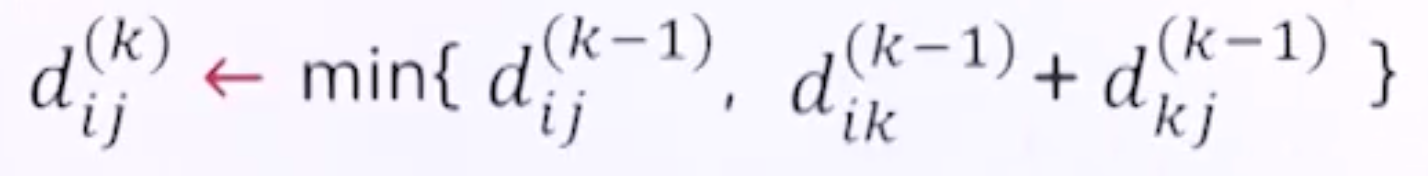
-
-
-
- G = (V,E), |V| = n
- D(i, j, 0)
- 정점 i에서 정점 j까지 경유하는 정점 없이 간선으로 직접 연결된 경로의 길이
- D(i, j, 0) = dij^(0) = wij (1<=i, j<=n)
- D(i, j, k)
- 정점 i에서 정점 j까지의 경로 중에서 정점 1부터 k까지의 정점만을 경유할 수 있는 최단 경로의 길이
- D(i, j, k) = dik^(k) = min[dij^(k-1), dik^(k-1)+dik^(k-1)]
- D(i, j, 0)
- 성능 분석
- O(n^3)
- G = (V,E), |V| = n
-
-

-
- 저울 문제
- 양팔 저울, n 개의 추, 각 추의 무게 wi(1<=i<=n)
- 무게 M인 물체를 양팔 저울로 달 수 있는지 확인하는 문제
- 최적성의 원리
- n개의 추로 무게 M인 물체를 확인하는 문제
- k개의 추(s1, s2, s3, ..., sk)가 선택 -> M = ws1 + ws2 + ... + wsk
- 선택된 추에 n번 추가 포함되지 않는다면
- 1 ~ (n-1)번 까지의 추를 이용하여 무게 M인 물체를 달 수 있는지의 문제
- 선택된 추에 n번 추가 포함된다면 (Sk = n이라고 가정)
- n번 추를 제외시키면 ws1 + ws2 + ... + wsk-1 = M - wsk
- 1 ~ (n-1)번까지의 추를 이용하여 무게 M-wsk인 물체를 달 수 있는지의 문제
- 점화식
- S(i, k) = 1 또는 0
- 1번부터 i번까지의 추를 이용하여 무게 k인 물체를 달 수 있는지의 여부
- S(i, k) = max[S(i-1, k), S(i-1, k-wi)] 1<=i<=n, 1<k<=M
- S(n, M) = ?
- S(i, k) = 1 또는 0
- 성능
- O(nM) 있음
- 특징
- 무게 K의 증가를 추의 무게의 최대공약수 단위로 증가시키면 더 효율적
- 테이블 S와 wi(1<=i<=n)를 이용하면 사용된 추를 구할 수 있음
- S(n-1, M-wn) = 1 -> n번추 사용
- S(n-1, M) = 1 -> n번추 미사용
- 물체의 무게가 2^n보다 크면 모든 경우를 따져 보는 직관적인 방법보다 비효율적
- 직관적 알고리즘: n개의 추로 조합 가능한 모든 경우의 수 -> O(2^n)
- M > 2^n이면 nM > n2^n > 2^n이므로 O(nM)인 알고리즘이 직관적인 알고리즘보다 비효율적
- M과 wi가 정수가 아니면 동적 프로그래밍 방법 적용
- n개의 추로 무게 M인 물체를 확인하는 문제
- 저울 문제
'algorithm' 카테고리의 다른 글
| [algorithm] 1952 달팽이 java (0) | 2021.04.14 |
|---|---|
| [algorithm] 달팽이 java (0) | 2021.04.13 |
| 동적프로그래밍 알고리즘 (0) | 2021.04.09 |
| [algorithm] 전화번호 목록 (0) | 2021.04.03 |
| [algorithm] 완주하지 못한 선수 java (0) | 2021.04.03 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 인접리스트
- 최단경로
- 운영체제
- 이진탐색
- 자료구조
- client side rendering
- 배열
- dfs
- 클래스
- 알고리즘
- 동적프로그래밍
- 병행프로세스
- C
- 교착상태
- Stack
- 재귀함수
- Java
- 퀵정렬
- 구조체
- 세마포어
- C++
- 스텍
- javascript
- 인접행렬
- server side rendering
- 소프트웨어
- 입출력장치
- BFS
- stackframe
- react
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함
