티스토리 뷰
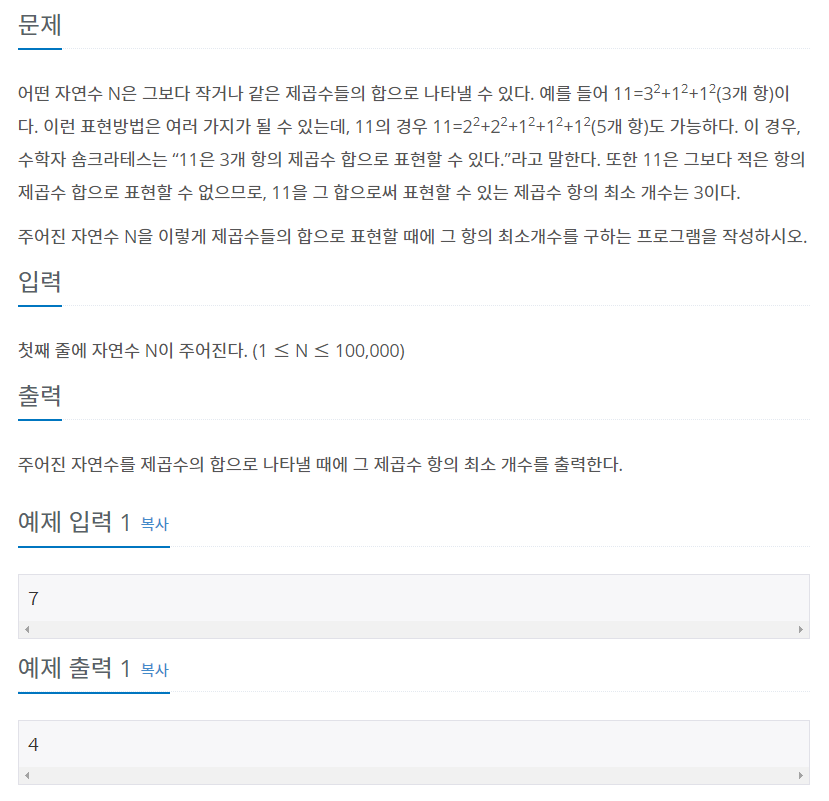
이 문제는 제곱수의 합을 구하는 문제로
처음에는 하나씩 더하기 형식으로 써내려가다보니 마지막 끝나는 자리로 푸는 것인가해서 이러한 방법으로 접근했으나 아니었다..
dp문제는 항상 이전 배열의 수를 어떻게 사용할지를 먼저 보는것이 포인트라면 포인트 인 것 같다.
일단 dp배열에는 내가 구하는 답이 들어간다는 사실을 잊지말자
예를들어 dp[4]에는 4를 제곱수 합으로 표현할 수 있는 최소값이 들어간다.
- 방법정리
- i는 n까지 루프를 돈다.
- j는 i까지 루프를 돈다.
- 단 j의 제곱은 i를 넘길 수 없으므로 j * j가 i를 넘지 않는 범위까지 루프를 돈다.
- dp[i] 에는 기본값으로 i를 넣는다.
- 1을 i만큼 더하면 제곱수를 최대로 넣는셈
- dp[i] 에 기본값으로 i가 들어가 있으니 그 다음부턴 1보다 큰 j를 제곱해서 i에서 빼면 처음 dp[i]보다는 무조건 값은 값이 나온다.
- j*j 값이 i를 넘지 않는 범위에서 최대일 때 거기에 +1을하면 dp[i]의 값이 나온다.
public class Main {
static int dp[], arr[];
static int max;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new int[n+1];
dp[1] = 1;
for(int i = 2; i < n+1; i++) {
dp[i] = i;
sc.close();
for(int j = 1; j*j <= i; j++) {
dp[i] = Math.min(dp[i], dp[i-j*j]+1);
}
}
System.out.println(dp[n]);
}
}'algorithm' 카테고리의 다른 글
| [DP] 9461 파도반수열 (0) | 2020.05.01 |
|---|---|
| [DP] 2133 3*n 타일링문제 (0) | 2020.05.01 |
| [DP] 2579 런타임에러 (0) | 2020.04.27 |
| [DP] 2156 (0) | 2020.04.23 |
| [DP] 9465, 2156 (0) | 2020.04.22 |
댓글
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- react
- stackframe
- dfs
- 병행프로세스
- Java
- 클래스
- 교착상태
- 동적프로그래밍
- C++
- client side rendering
- C
- Stack
- 소프트웨어
- 배열
- 운영체제
- 구조체
- 재귀함수
- javascript
- 이진탐색
- server side rendering
- 스텍
- 인접리스트
- 입출력장치
- 알고리즘
- 인접행렬
- 최단경로
- 자료구조
- 퀵정렬
- 세마포어
- BFS
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
글 보관함
